تمارين متنوعة على الوحدة السادسة الصف الحادي عشر الرياضيات الأساسية إعداد: الأستاذة فاطمة الزهراء السيد

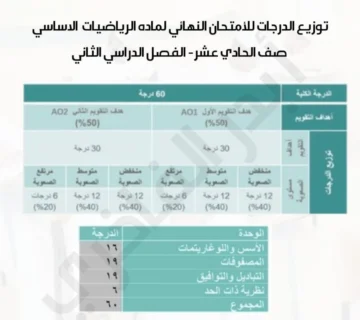
تعتبر تمارين متنوعة على الوحدة السادسة الصف الحادي عشر من الموضوعات الأساسية في علم الرياضيات، حيث تستخدم في مجالات متعددة مثل الفيزياء، الهندسة، والاقتصاد/ تساعد هذه المفاهيم في تبسيط العمليات الحسابية المعقدة، خاصة عند التعامل مع الأعداد الكبيرة والصغيرة جدًا.

تمارين متنوعة على الوحدة السادسة  الصف الحادي عشر الرياضيات الأساسية

• موضوع الوحدة: الأسس واللوغاريتمات
• تمارين متنوعة لاختبار الفهم والتدريب على التطبيقات المختلفة.
• أسئلة متعددة الاختيارات لتعزيز الفهم السريع للمفاهيم.
• تمارين حسابية وتطبيقية لحل المعادلات اللوغاريتمية والأسية.
• مراجعة شاملة تساعد الطلاب على الاستعداد للاختبارات.

مفهوم الأسس واللوغاريتمات

 الأسس (Exponents)

• الأس هو عدد يحدد عدد المرات التي يتم فيها ضرب الرقم بنفسه

اللوغاريتمات (Logarithms)

اللوغاريتم هو العملية العكسية للأسس، وهو يعبر عن الأس الذي يجب أن يُرفع له العدد للحصول على قيمة معينة. يُكتب بالشكل التالي:

log⁡b(x)=y⇔by=x\log_b (x) = y \quad ⇔ \quad b^y = xlogb​(x)=y⇔by=x

حيث

• bbb هو الأساس.
• xxx هو العدد.
• yyy هو القيمة اللوغاريتمية.

أمثلة

• log⁡2(8)=3\log_2 (8) = 3log2​(8)=3 لأن 23=82^3 = 823=8.
• log⁡10(1000)=3\log_{10} (1000) = 3log10​(1000)=3 لأن 103=100010^3 = 1000103=1000.

قوانين الأسس واللوغاريتمات

هناك عدة قوانين مهمة تساعد في تبسيط الحسابات، ومنها:

 قوانين الأسس

1. الضرب في الأسس المتشابهة: am×an=am+na^m \times a^n = a^{m+n}am×an=am+n
2. القسمة في الأسس المتشابهة: aman=am−n\frac{a^m}{a^n} = a^{m-n}anam​=am−n
3. رفع القوة إلى قوة أخرى: (am)n=am×n(a^m)^n = a^{m \times n}(am)n=am×n
4. الأس السالب: a−n=1ana^{-n} = \frac{1}{a^n}a−n=an1​
5. الأس الصفري: a0=1a^0 = 1a0=1

 قوانين اللوغاريتمات

1. لوغاريتم حاصل الضرب: log⁡b(A×B)=log⁡bA+log⁡bB\log_b (A \times B) = \log_b A + \log_b Blogb​(A×B)=logb​A+logb​B
2. لوغاريتم القسمة: log⁡b(AB)=log⁡bA−log⁡bB\log_b \left(\frac{A}{B}\right) = \log_b A – \log_b Blogb​(BA​)=logb​A−logb​B
3. لوغاريتم القوة: log⁡b(An)=nlog⁡bA\log_b (A^n) = n \log_b Alogb​(An)=nlogb​A
4. التحويل بين الأسس المختلفة: log⁡aB=log⁡cBlog⁡cA\log_a B = \frac{\log_c B}{\log_c A}loga​B=logc​Alogc​B​

تطبيقات الأسس واللوغاريتمات في الحياة اليومية

 1. في العلوم والهندسة

• تستخدم اللوغاريتمات في قياس الزلازل من خلال مقياس ريختر، حيث قوة الزلزال تُحسب باستخدام اللوغاريتمات العشرية.
• تساعد الأسس في حساب نمو البكتيريا في المختبرات العلمية.

 2. في الاقتصاد والمالية

• تُستخدم اللوغاريتمات في حساب الفائدة المركبة في البنوك، حيث يتم حساب نمو الأموال بمرور الوقت باستخدام الصيغ اللوغاريتمية.
• تساعد في تحليل الاستثمارات المالية وتوقع أداء الأسهم والسندات.

 3. في تكنولوجيا المعلومات والاتصالات

• تستخدم في تشفير البيانات والذكاء الاصطناعي.
• تعتمد بعض الخوارزميات على اللوغاريتمات لحل المشكلات بسرعة وكفاءة.

كيفية الاستفادة من كراسة التمارين؟

•  ابدأ بحل التمارين الأساسية للتأكد من فهم القوانين والمفاهيم.
•  استخدم القوانين لتبسيط العمليات الحسابية بدلاً من إجراء حسابات طويلة.
•  جرب حل التمارين الصعبة دون النظر إلى الحلول، ثم قارن إجابتك مع النموذج الصحيح.
•  قم بحل التمارين الإضافية الموجودة في الكراسة لاختبار مستواك الحقيقي.
•  إذا واجهتك أي صعوبة، حاول مراجعة المفاهيم الأساسية قبل الانتقال إلى المسائل المعقدة.

تعتبر الأسس واللوغاريتمات من أهم المفاهيم في الرياضيات، ولها تطبيقات واسعة في مختلف العلوم والمجالات العملية. فهم هذه القوانين يساعد في تسهيل العمليات الحسابية والتفكير المنطقي،  ومن خلال التدرب على التمارين المتنوعة، يمكن للطلاب تعزيز مهاراتهم في حل المشكلات الرياضية بكفاءة أكبر.

للمزيد للصف الحادي عشر ما يلي:

• المكتبة الإلكترونية للصف الحادي عشر الفصل الدراسي الثاني النسخة الأدبية إعداد الطالب عبدالله يسري
• الصف الحادي عشر الفصل الثاني
• الرياضيات الأساسية